-
[pytorch] NLLLoss 알아보기 (Negative Log Likelihood)AI-ML 2024. 2. 22. 20:39반응형
- 목차
키워드.
- - Likelihood
- - NLL Loss
Likelihood 란 ?
이번 글의 주제인 NLL Loss 의 NLL 은 Negative Log Likelihood 의 약자입니다.
그래서 우선적으로 Likelihood 의 의미에 대해서 간략히 알아보려고 합니다.
Likelihood 는 우리말로 가능성, 가능도, 우도 등으로 불립니다.
Likelihood 는 수식으로 아래와 같이 표현됩니다.
$$ L(\theta | x) $$
$ \theta $ 는 모델의 파라미터 또는 확률 분포의 여러 변수들을 의미하구요.
그리고 X 는 데이터 또는 Random Variable 을 의미합니다.
정확한 이해를 위해서 여러가지 예시를 설명드리겠습니다.
정규 분포와 Likelihood.
대한민국 성인 남성의 키를 정규분포로 표현한다고 가정하겠습니다.
이는 키라는 값은 연속적으로 존재하는 일련의 실수이기 때문에 연속 확률 분포를 가집니다.
그리고 연속 확률 분포는 일반적으로 정규 분포를 취하게 되죠.

정규 분포는 2가지의 종류한 파라미터를 가집니다.
바로 평균과 표준편차입니다.
아래의 그림에서 노란색의 정규 분포는 평균이 172cm, 표준 편차가 4.8cm 인 파라미터를 가집니다.
그리고 녹색의 정규분포는 평균이 184cm 인 상태를 표현하죠.

반면 표준 편차가 증가하게 되면 아래와 그래프와 같이 가로폭이 넓은 정규 분포가 생성됩니다.
붉은 색의 그래프에 비해서 녹색의 그래프의 표준 편차가 더 큰 정규 분포를 의미합니다.
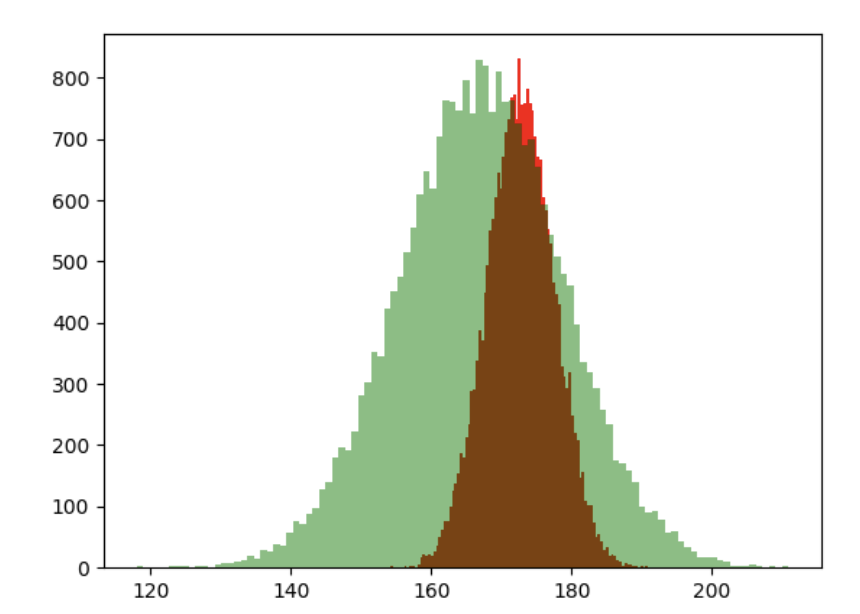
정리하면, 신장과 같은 연속 확률 변수는 일반적으로 정규 분포를 따르게 됩니다.
그리고 정규 분포는 평균과 표준 편차라는 2개의 파라미터를 가지며,
총 500명의 성인 남성의 키가 160cm ~ 190cm 의 범위를 가지고 평균이 172cm & 표준 편차가 4.8cm 하고 한다면,
이러한 샘플 데이터를 가장 잘 표현할 수 있는 정규분포는 아래의 정규 분포를 의미하게 됩니다.

이를 Likelihood 관점에서 이야기하면,
무작위로 추출된 500명의 성인 남성의 키를 가장 잘 표현할 수 있는 정규분포는 평균이 172cm & 표준 편차가 4.8cm 인 정규분포이며,
$$ Optimal Likelihood = L( \theta | x ) ; \mu = 172, \delta = 4.8 $$
인 상황이 됩니다.
모델과 Likelihood.
정규 분포와 Likelihood 는 최적의 데이터 분포를 탐색하기 위한 Likelihood 였다면,
머신러닝의 관점에서 Likelihood 의 개념 또한 존재하며, 이는 정규 분포와 Likelihood 와 유사합니다.
선형회귀를 수행하는 간단한 모델이 있다고 가정하겠습니다.
그리고 이 모델의 수식은 아래와 같습니다.
$$ \hat{y} = \beta_{1}x_{1} + \beta_{2}x_{2} + ... + \beta_{n}x_{n} $$
예측값 Y 를 계산하기 위해서 n 개의 파라미터와 n 개의 데이터가 연산에 사용됩니다.
선형 회귀 문제는 Loss Function 을 최소화하는 방향으로 파라미터들을 조금씩 수정해나가는데요.
최소의 Loss 를 만드는 Parameter 가 선형 회귀 모델의 최적의 파라미터로 사용됩니다.

출처 : https://www.analyticsvidhya.com/blog/2021/04/gradient-descent-in-linear-regression/ 최적의 파라미터를 가지는 모델은 Likelihood 가 가장 높다고 표현할 수 있습니다.
왜냐하면 주어진 Data 에 가장 Fit 한 Parameter 가 데이터를 가장 잘 표현할 수 있기 때문입니다.
사실상 머신러닝 분야에서는 Overfit 을 방지하기 위해서 일부러 학습을 방해하는 요소를 추가하곤 합니다. (Regularization)
그래서 Overfit 의 파라미터가 Likelihood 는 높을수는 있어도 최적의 파라미터는 아니지만,
중요한건 모델에서의 Likelihood 가 데이터 분포의 Likelihood 와 크게 다른 의미를 가지진 않습니다.
Likelihood 에 대해서 간단히 정리하면.
Likelihood 는 주어진 데이터를 특정 파라미터가 얼마나 데이터를 잘 표현하는지를 수치화시키는 개념입니다.
성인 남성 500명의 데이터가 주어졌을 때에, 이를 가장 잘 표현하는 평균과 표준 편차가 172cm, 4.8cm 였던것처럼 말이죠.
만약 평균이 140cm, 표준 편차가 10cm 인 정규 분포는 매우 안좋은 Likelihood 수치를 가질 것입니다.
평균이 190cm, 표준 편차가 1cm 인 정규 분포 또한 매우 안좋은 Likelihood 수치를 가지겠죠 ?
이처럼 Likelihood 는 특정 파라미터가 데이터를 얼마나 잘 표현하는지에 대한 정도임을 알아두시면 좋을 것 같습니다.
Negative Log Likelihood.
Negative Log Likelihood 는 Negative 와 Log, Likelihood 를 각각 나누어서 생각하면 이해하기 수월합니다.
Negative 는 말 그대로 마이너스 부호 (-) 를 취함을 뜻합니다.
즉, -1 를 곱하죠.
그리고 Log 또한 말 그대로 Logarithm 연산을 취한다는 의미합니다.
종합해보면, Likelihood 값에 마이너스 연산과 Logarithm 연산을 취한다는 의미합니다.
그래서 수학적인 관점에서 만약 Likelihood 가 0.5 라면, -log(0.5) 연산을 취함을 뜻합니다.
pytorch 에서 NLL Loss.
하지만 pytorch 에서 사용되는 NLL Loss 는 사용법이 조금 다릅니다.
pytorch 의 NLLloss 는 아래와 같이 사용됩니다.
nn.NLLLoss() 함수를 사용하여 Negative Log Likelihood 함수를 생성합니다.
그리고 soft_max_output 이라는 Tensor 를 하나 생성합니다.
soft_max_output 이라고 이름을 붙인 이유는 Softmax Layer 에 의해서 출력되는 Tensor 임을 표현하기 위함입니다.
이는 [0.1, 0.1, 0.8] 이라는 출력값을 가지는데요.
이 의미는 3개의 분류 중에서 첫번째와 두번째로 분류될 확률이 0.1, 그리고 세번째 분류가 될 확률이 0.8 임을 의미합니다.
그리고 NLL Loss 를 의 결과는 -0.1, -0.1, -0.8 이 됩니다.
import torch import torch.nn as nn loss_function = nn.NLLLoss() soft_max_output = torch.tensor([[0.1, 0.1, 0.8]], dtype=torch.float32) label1 = torch.tensor([0]) label2 = torch.tensor([1]) label3 = torch.tensor([2]) print(f'label1 loss is {loss_function(soft_max_output, label1).item()}') print(f'label2 loss is {loss_function(soft_max_output, label2).item()}') print(f'label3 loss is {loss_function(soft_max_output, label3).item()}')label1 loss is -0.10000000149011612 label2 loss is -0.10000000149011612 label3 loss is -0.800000011920929사실상 pytorch 에서의 NLL Loss 는 예측 확률과 실제 확률을 곱하고 음수로 표현하는 것이 지나지 않습니다.
수식으로 표현하면 아래와 같습니다.
$$ NLL Loss = - (\hat{y} * y) $$
아주 단순하죠 ?
이는 Cross Entropy Loss 와 비교되는 중요한 Loss Function 중의 하나입니다.
pytorch 에서는 Softmax Layer 를 생략하거나 명시할 수 있도록 CrossEntropyLoss 와 NLLLoss 두가지 함수가 제공됩니다.
CrossEntropyLoss 를 사용하게 되는 경우에는 Softmax Layer 를 생략할 수 있습니다.
반면, NLLLoss 를 사용하는 경우에는 Softmax Layer 가 반드시 명시되어야 합니다.
pytorch 에서의 Negative Log Likelihood 에서는 Logarithm 연산이 사용되지 않는 함정이 있음에 유의하시면 좋을 것 같네요.
반응형'AI-ML' 카테고리의 다른 글
pytorch - Conv2D 알아보기 ( CNN ) (0) 2024.03.03 [torchvision] ToTensor 알아보기 (0) 2024.03.01 Sigmoid Activation Saturation 알아보기 (0) 2024.01.10 [PyTorch] RNN 모듈 알아보기 (0) 2023.12.29 Covariate Shift 알아보기 (0) 2023.12.24